Contoh Contoh Soal

Soal Rangkaian Listrik Kompleks

1. Carilah Nilai I ?

Jawab:

Bila kita melihat resistor R1, R2, dan R3 sebagai suatu rangkaian Δ (pada rumus berturut-turut Rab, Rac, dan Rbc) dan ingin menggantinya dengan rangkaian Y, kita bisa mengubah rangkaian jembatan ini menjadi rangkaian yang lebih sederhana yaitu rangkaian seri-paralel:

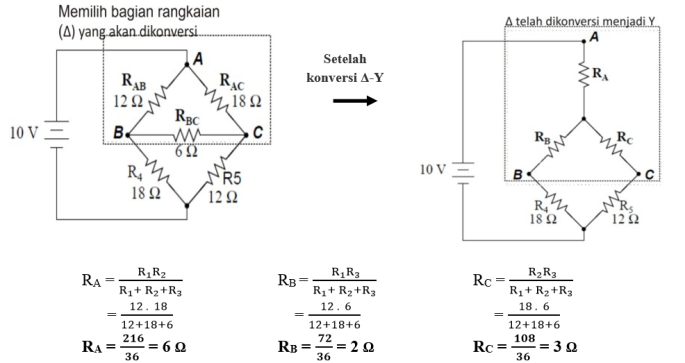
Sekarang kita telah mendapatkan rangkaian yang lebih sederhana. Kita bisa menganalisa rangkaian ini menggunakan aturan seri-paralel:

Serikan rangkaian RB dan R4 serta rangkaian Rc dan R5

RS1 = RB + R4

        = 2Ω + 3Ω = 5 Ω

RS2 = RC + R5

        = 3Ω + 12Ω = 15 Ω

sehingga terbentuk rangkaian seperti ini:

Selanjutnya, hambatan RS1 dan RS2 di paralelkan

RS1// RS2 = RP =

Rp =  =  = 3 Ω

Dan terbentuk rangkaian seri seperti ini :

Dan rangkaian diatas dihitung secara seri menjadi RT

RT = RA  + RP

                               = 6 + 3 = 9 Ω

Lalu, hitung I dengan menggunakan hukum Ohm

2. Pada rangkaian listrik berikut ini, tentukanlah daya yang melalui hambatan R3.

Diketahui ε1 = 8V, ε2 = 8 V, ε3 = 2V. Harga masing-masing hambatan adalah
R1 = 5 Ω , R2 = 1 Ω, R3 = 2 Ω, R4 = 1 Ω, dan R5 = 5 Ω.

Pembahasan :
Seperti yang telah diuraikan di atas, terlebih dahulu kita tentukan arah loopnya.
Lihat bahwa ggl kedua (ε2) yang berada di tengah nilainya lebih kecil dari ggl
lainnya sehingga asumsikanlah arah loopnya menuju ke tengah seperti berikut ini.

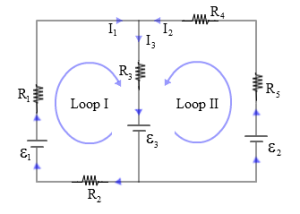
Dari gambar jelas terlihat bagaimana hubungan antara arus pada titik percabangan yaitu : I3 = I1 + I2

Selanjutnya tinjaulah masing-masing loop.

Tinjau Loop I
∑ ε + ∑ I.R = 0
⇒ ε1 + ε3 + (R1 + R2) I1 + R3.I3 = 0
⇒ -8 + 2 + 6 I1 + 2 I3 = 0
⇒ -6 + 6 I1 + 2 (I1 + I2) = 0
⇒ -6 + 6 I1 + 2 I1 + 2 I2 = 0
⇒ -6 + 8 I1 + 2 R2 = 0
⇒ 8 I1 + 2 I2 = 6
⇒ 4 I1 + I2 = 3
⇒ I2 = 3 – 4 I1

Tinjau Loop II
∑ ε + ∑ I.R = 0
⇒ ε2 + ε3 + (R4 + R5) I2 + R3.I3 = 0
⇒ -8 + 2 + 6 I2 + 2 I3 = 0
⇒ -6 + 6 I2 + 2 (I1 + I2) = 0
⇒ -6 + 6 I2 + 2 I1 + 2 I2 = 0
⇒ -6 + 8 I2 + 2 I1 = 0
⇒ 8 I2 + 2 I1 = 6
⇒ 4 I2 + I1 = 3
⇒ I1 + 4 I2 = 3

Dari dua persamaan yang telah kita peroleh, tentukan nilai I1 dan I2 dengan metode eliminasi ataupun substitusi.
Dengan substitusi diperoleh :
I1 + 4 I2 = 3
⇒ I1 + 4 (3 – 4 I1)= 3
⇒ I1 + 12 – 16 I1 = 3
⇒ -15 I1 = 3 – 12
⇒ -15 I1 = -9
⇒ I1 = 9⁄15
⇒ I1 = 3⁄5 A.
Dengan begitu diperoleh arus kedua :
I2 = 3 – 4 I1
⇒ I2 = 3 – 4 (3⁄5)
⇒ I2 = 3 – 12⁄5
⇒ I2 = 15⁄5 – 12⁄5
⇒ I2 = 3⁄5 A.
Berdasarkan hukum Kirchoff I,
maka nilai I3 diperoleh :
I3 = I1 + I2
⇒ I3 = 3⁄5 + 3⁄5
⇒ I3 = 6⁄5 A
Dengan begitu, daya yang melalui hambatan R3 adalah :
P = I32 R3
⇒ P = (6⁄5)2 (2)
⇒ P = 36⁄25 (2)
⇒ P = 2,88 Watt.

Soal Hukum Ohm

1. Berdasarkan data pada tabel, nilai hambatan listrik adalah….. Apakah data pada tabel menggambarkan hukum Ohm ?

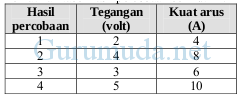
Pembahasan

R = V / I = 2 volt / 4 Ampere = 1/2 Ω

R = V / I = 4 volt / 8 Ampere = 1/2 Ω

R = V / I = 3 volt / 6 Ampere = 1/2 Ω

R = V / I = 5 volt / 10 Ampere = 1/2 Ω

Menurut hukum Ohm, V/I konstan. Jadi isi tabel di atas menjelaskan hukum Ohm.

Soal Hukum Kirchoff I

Perhatikan gambar di atas, pada titik P dari sebuah rangkaian listrik ada 4 cabang, 2 cabang masuk dan 2 cabang keluar. Jika diketahui besarnya I1 = 6 A, I2 = 3 A, dan I3 = 7 A, tentukan berapa besar nilai dari I4?

Jawab

Diketahui

I1 = 6A
I2 = 3 A
I3 = 7 A

Ditanya I4 = …?
Hukum Kirchoff I

ΣImasuk = ΣIkeluar

I1 + I2 = I3 + I4
6 + 3 = 7 + I4
9 = 7 + I4
I4 = 9-7 = 2A

Soal Hukum Kirchoff II

Tentukan: 

a. Kuat arus yang mengalir

b. Tegangan Antara

jawab:

a. Misalkan arah kuat arus kita anggap dulu berlawanan dengan arah loop

Σε + ΣI. R = 0
ε3 – ε2 + ε1 – I (R1 + R2 + R3) = 0
4 – 2 + 4 – I (15 + 5 + 10) = 0
6 – 30I = 0
30I = 6
I = 6/30 = 1/5 = 0,2 A

b. Tegangan antar a dan b (Vab)

Jika melalui jaluar adcb (panjang)
Vab = ε3 – ε2 – I (R3 + R2) (I negatif karena berlawanan dengan arah I total)
Vab = 4-2 – 0,2 (10 + 5)
Vab = 2 – 0,2 (15)
Vab = 2 – 3 = -1 V

Jika melalui jalur ab (pendek)
Vab = -ε1 + I R1 ( I positif karena searah dengan I total)
Vab = – 4 +  0,2 (15)
Vab = -4 + 3 = -1 V
Jadi tegangan antara titi  a dan b (Vab) = -1 V

Soal Hukum Elemen Aktif 

1. R1 = 2 Ω, R2 = 4 Ω, R3 = 6 Ω, R4 = 8 Ω, V = 12 Volt. Tentukan (a) Nilai resistor pengganti (b) Arus listrik yang mengalir pada rangkaian (c) Arus listrik yang mengalir melalui resistor R2 (d) Tegangan listrik pada kedua ujung resistor R4.

Pembahasan

(a) Resistor pengganti

R = R1 + R2 + R3 + R4 = 2 + 4 + 6 + 8 = 20 Ω

(b) Arus listrik

I = V / R = 12 volt / 20 Ω = 0,6 volt/Ω = 0,6 Ampere

(c) Arus listrik yang melewati resistor R2

Menurut hukum I Kirchhoff, tidak ada titik cabang sehingga arus listrik yang melewati rangkaian = arus listrik yang melewati resistor R2 = 0,6 Ampere.

(d) V = I4 R4 = (0,6 A)(8 Ω) = 4,8 Volt.

Soal Hukum Elemen Pasif 

Resistor 

1. Diketahui rangkaian listrik seperti di bawah ini, dimana V=45V. Tentukan arus, jatuh tegangan melintas resistor, dan daya pd masing-masing2 resistor!

Induktor 

Berdasarkan gambar contoh rangkaian Paralel Induktor diatas, diketahui bahwa nilai Induktor :

L₁ = 100nH
L₂ = 300nH
L₃ = 30nH
L_total= ?

Penyelesaiannya

1/L_total = 1/L₁ + 1/L₂ + 1/L₃ 
1/L_total = 1/100nH + 1/300nH + 1/30nH
1/L_total = 3/300 + 1/300 + 10/300
1/L_total = 14/300
1/L_total = 14 x L = 1 x 300 (hasil kali silang)
1/L_total = 300/14
1/L_total = 21,428nH

Kapasitor 

1. Tiga kapasitor C1, C2 dan C3 dirangkai paralel, di mana masing-masing kapasitor mempunyai kapasitas 4 mikroFarad, 2 mikroFarad, 3 mikroFarad. Ketiga kapasitor diisi muatan listrik hingga kapasitor C2 mempunyai beda potensial 4 Volt. Tentukan (a) Muatan listrik pada kapasitor C1, C2dan C3 (b) Muatan listrik pada kapasitor pengganti ketiga kapasitor
Pembahasan
Diketahui :

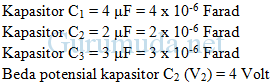
Ditanya : Muatan listrik pada kapasitor C3 (Q3)

penyelesaian:

(a) Muatan listrik pada kapasitor C3 
Beda potensial pada kapasitor C3 :
Kapasitor dirangkai paralel karenanya beda potensial pada kapasitor C3 (V3) =  beda potensial pada kapasitor C2 (V2) = beda potensial pada kapasitor C1 (V1) = beda potensial pada kapasitor pengganti (V) = 4 Volt
Muatan listrik pada kapasitor C1:

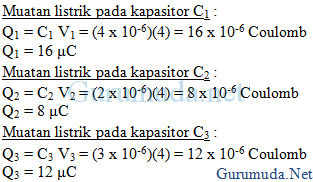
Muatan listrik pada kapasitor C2:

Muatan listrik pada kapasitor C3:

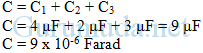
(b) Muatan listrik pada kapasitor pengganti ketiga kapasitor   
Cara 1 :

Cara 2 :